Discrete FFT for Character Bit Patterns
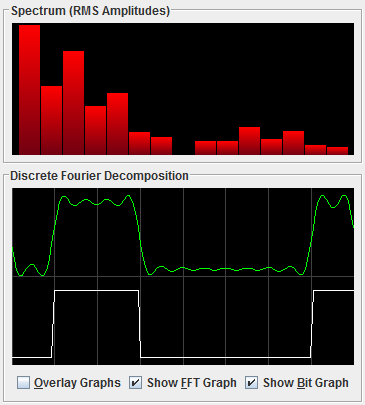
Screenshot of FFT applet.
This Discrete FFT applet was written for my networking class during the Fall 2000 semester. The information about Fourier analysis found below appears in Andrew S. Tanenbaum's Computer Networks, 3rd Ed., Prentice-Hall, Inc., 1996.
Download executable JAR:
FFT.jar
Background
In the early 19th century, French mathematician Jean-Baptiste Fourier proved that any reasonably behaved periodic function, g(t), with period T can be constructed as a (possibly infinite) sum of sines and cosines:
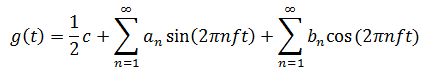
where f = 1/T is the fundamental frequency, and an and bn are the sine and cosine amplitudes of the nth harmonics. The formulas for the amplitudes of the harmonics and DC component follows:
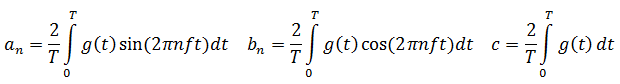
The root-mean-square amplitudes, 
, which are displayed in the red bar graph, are of interest because their squares are proportional to the energy transmitted at the corresponding frequency.
There are no means of transmitting signals without losing some power in the process. If all the Fourier components were equally diminished, the resulting signal would be reduced in amplitude but not distorted. However, this is not the case because all transmission facilities diminish different Fourier components by different amounts. After studying this topic and analyzing the graphs, it should be clear that there is no hope for binary signals at data rates higher than 38.4 kbps, even if the transmission facility is noiseless. Fortunately, sophisticated coding schemes that use several voltage levels do exist and can achieve higher data rates.
This applet shows a binary signal and its root-mean-square Fourier amplitudes with an approximation to the original signal based on the user's input.